What is the Multiplicative Inverse Calculator
Multiplicative inverse calculator with steps is a digital tool that is used to find the multiplicative inverse of a given number in a fraction of a second. It computes various types of numbers(natural numbers, fractions, negative numbers) and finds their inverse value.

It is a beneficial tool for everyone because some numbers are confusing so it is difficult to find that number multiplicative inverse. You can get rid of all these difficulties and use our multiplicative inverse solver that gives you solutions in just one click.
What is a Multiplicative Inverse
Multiplicative inverse is defined as the number which is the reciprocal of a given number. When you multiply the reciprocal number with the given original number its product gives 1 number in solution. It is called multiplied inverse or reciprocal.
If x is the original number then its inverse is 1/x or x^-1. The multiplicative inverse is one of the properties of set theory that defines whether the given set of numbers is a group or not. Nevertheless, multiplicative inverse property can be applied to numbers like fractions, integers, or other sets of numbers.
What is the Inverse Property of Multiplication
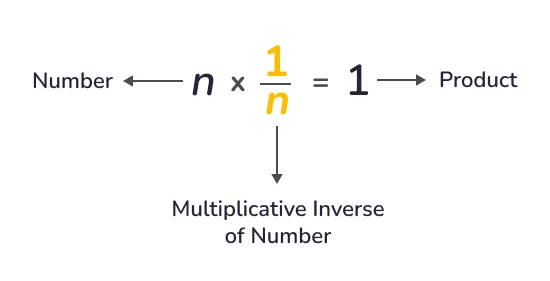
Multiplicative inverse property is the basic property used in algebra but it is commonly used in set theory, group, ring, or field. Here n is the given number,
- 1/n is the reciprocal or multiplicative inverse of a given number n
- 1 is the product result when you multiply number or its multiplicative inverse.
How to Find Multiplicative Inverse
To find the multiplicative inverse, the online Multiplicative inverse calculator usually uses the simple method for any type of given number. Let's see some rules that are used for different numbers to find their reciprocal or inverse. These rules are:
For Natural Number
Let's define natural numbers to find multiplicative inverse with the help of an example. For example, 6 is the natural number so its inverse is 1/6. When you multiply 6 with 1/6 it gives a solution is 1. Similarly, you can take any number like 9 so its multiplicative inverse is 1/9.
For Fraction
The multiplicative inverse of the fraction is the reciprocal of that fraction. For example 2/3 multiplicative inverse is 3/2 because when we multiply fraction and its multiplicative inverse. it gives the product result 1, as it satisfies the multiplicative rule.
For Mixed Fraction
Mixed fraction multiplication is different than integers or natural numbers because inverse multiplication calculator first solves the mixed fraction into simple ones and then find its multiplicative inverse. For example 3-2/4 converts into a simple fraction of 14/4. The inverse multiple of 14/4 is 4/14.
For Negative Number
Negative number multiplicative inverse is also negative. For example -3 inverse multiplicative is -1/3 because when we multiply them it gives solution 1.
On the other hand, when you give the multiplicative inverse of -3 as ⅓ then the inverse multiplicative calculator gives its product as -1 which does not satisfy the multiplicative inverse rule. It is noted that you should put the negative sign with the numerator, not with the denominator.
What is the Multiplicative Inverse of ½
The multiplicative inverse of ½ is 2/1. If you give the multiplication inverse calculator a denominator 1 or write the number 2 only then it doesn't matter because 1 denominator number has no importance. We consider it only 2 in mathematics.
$$ \frac{1}{2} \times 2 \;=\; 1 $$
Therefore the multiplicative inverse of ½ is always 2.
What is the Multiplicative Inverse of 5
The multiplicative inverse of 5 is 1/5. As it satisfies the multiplicative inverse property rule when you multiply 5*1/5 the answer is 1.
Therefore the multiplicative inverse of 1/5 is always 5.
What is the Multiplicative Inverse of ⅔
The multiplicative inverse of 2/3 is 3/2. As it satisfies the multiplicative inverse property rule when you multiply 2/3*3/2 the answer is 1.
Therefore the multiplicative inverse of 2/3 is always 3/2.
How to Use the Multiplicative Inverse Calculator
Multiplicative inverse solver has a user-friendly design tool that enables you to calculate the Multiplicative inverse of specific numbers. Before using our calculator, you must follow some simple steps, and you do not face any inconvenience during the calculation. These steps are:
- Enter your number's value in the input box.
- Review your input number before hitting the calculate button to start the evaluation process in the inverse multiplication calculator
- Click the “Calculate” button to get the result of your given number problem for reciprocal or multiplicative inverse.
- You should try out the inverse multiplicative calculator, first, you can use the load example so that you must be assured that it provides an accurate solution.
- Click on the “Recalculate” button to get a refresh page for more solutions for multiplication inverse calculator question solution
Output from Multiplicative Inverse Solver
Online Multiplicative inverse calculator gives you the solution of a given number problem when you add the input into it. It provides you with solutions with a detailed procedure to calculate multiplicative inverse from the number value instantly. It may contain as:
- Result Option
The result option gives you a solution for the Multiplicative inverse of a number problems
- Possible Steps
It provides you with a solution where all the evaluation processes are in a step-by-step method when you click on this option.
Advantages of Using Inverse Multiplication Calculator
The Multiplicative inverses calculator provides you with multiple benefits whenever you use it to calculate given numbers to find the multiplicative inverse of a number. These benefits are:
- Multiplicative inverse solver is a free-of-cost tool so you can use it anytime to find the multiplicative inverse from a given number problem in real time without spending anything.
- It is a handy tool as it can handle various types of methods to find the reciprocal of given questions.
- You can try out our inverse multiplicative calculator to practice new examples so that you get a strong hold on the inverse multiplicative concept
- Our tool saves you time and effort from doing confusing number problems to find the inverse multiplication problem.
- It is a reliable tool that provides you with accurate solutions whenever you use it for the evaluation of integers, fractions, or natural numbers without making any errors.
- Multiplicative inverse calculator with steps provides the solution with a complete process in a stepwise method so that you get clarity on the inverse multiplicative method.










