Introduction to Absolute Value Equations Calculator
Absolute Value Equations Calculator is a free online tool that helps you to find the absolute value for a given equation.

Our absolute value graph calculator evaluates the distance between two points in the absolute value of the variable and gives its solution in a fraction of a second.
What is the Absolute Value Equation?
The absolute value equation is defined as an algebraic equation inside the absolute bar symbol. This bar symbol is called the module or mode of a function. It is mostly used to find the distance between two points at a number line for example |x+3|.
An algebraic equation inside the mode is always a non-negative value equation if the value is in negative form but the mode makes it a positive value.
For example |-x| =|x|. On the other hand absolute value equation changes its nature into increasing or decreasing order when you solve the given equation.
Formula Used by Absolute Value Equation Calculator
There is no specific formula to find the Absolute value equation whether it consists of positive and negative values when we solve the mode value. It represents the result of the distance between two points (increasing or decreasing order).
Absolute value equation represents the result in a number line according to the given three cases. These cases are also used by our absolute value equations calculator which are as follow:
Case 1: x < a
If the value of x is less than a then the arrow goes toward the negative side graph line.
Case 2: a ≤ x < b
If the value of a is less than x and the value of b value is greater then the arrow goes in between the negative and positive sides of the graph line.
Case3: x ≥ b
If the value of x is greater than a then the arrow goes toward the positive side graph line.
$$ |x| \;=\; \biggr[ \begin{matrix} x, & x \ge 0 \\ -x, & x \lt 0 \\ \end{matrix} \biggr] $$
Working of Absolute Value Graph Calculator
The absolute value equations calculator uses the simplest method to solve the problem of the absolute value equation so that you can easily understand the concept of the absolute value equation instantly.
When you add the input value of an absolute value equation in our calculator with absolute value, it starts analyzing the given algebraic equation, for example, |4x+1|=7. After opening the module, the given equation is split in two with positive and negative signs respectively as 4x+1=7 and 4x+1=-7.
Then the absolute value equation solver solves the linear algebraic equation according to the rules of algebra and gives the solution in increasing and decreasing order as given in the below example x= 1.5 and x= -2.
Lastly, our absolute value equation calculator uses these points to draw an intersecting line on the graph so that you get a visual understanding of this concept.
Let's take an example solution of an absolute value equation from an absolute value functions calculator to check the working procedure behind this tool.
Example of the Absolute Value Equation
An example of an absolute value equation is given to know the manual calculations. As our absolute value equations calculator gives the solution in seconds but understanding its manual calculation is also important. So some examples are given below,
Example:
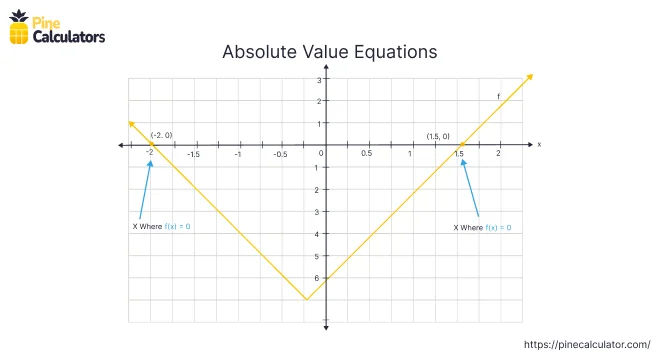
For the following function, determine the values of x such that f(x) = 0.
$$ f(x) \;=\; \biggr| 4x + 1 \biggr| - 7 $$
Solution:
$$ 0 \;=\; |4x + 1| - 7 $$
$$ 7 \;=\; |4x + 1| $$
$$ 7 \;=\; 4x + 1 \; \; \; \; or\; -7 \;=\; 4x + 1 $$
$$ 6 \;=\; 4x \; \; \; \; \; \; -8 \;=\; 4x $$
$$ x \;=\; \frac{6}{4} \;=\; 1.5 \; \; \; \; \; x \;=\; \frac{-8}{4} \;=\; -2 $$
How to Use the Absolute Value Equations Calculator?
The calculator with absolute value has the simplest layout that enables you to easily enter your input function. It will calculate the absolute value equation as per the rules for finding the absolute value equation immediately.
Follow some of our simple steps before using the absolute value equation calculator for evaluation so that you get a comfortable experience every time. These steps are:
- Enter the algebraic equation in the input field.
- Click on the “Calculate” button of absolute value graph calculator to get the solution of the absolute value equation problem.
- Review your algebraic expression before pressing the calculate button.
- Click on the “Recalculate” button to get a new page for more evaluation of the absolute value equation.
- If you want to check whether our tool gives you accurate results or not then you can first try out load example and get their solution to check the accuracy rate.
Result from Calculator with Absolute Value
The absolute value equations calculator provides you with the result of your given algebraic value problem in less than a minute after you hit the calculated button. It may include the following:
Result Option:
It provides you solutions for absolute value equations in both increasing and decreasing value.
Possible Steps:
It provides you with solutions for algebraic value equations in a step-wise process.
Number Line:
This option will draw a graph on the graph line as per the given result so that you understand it clearly.
Advantages of Absolute Value Equation Solver:
The absolute value equation calculator provides you with tons of benefits whenever you use it to calculate the absolute value equation in algebra for finding distance. These benefits are given below.
- The absolute value graph calculator saves the time and effort that you consume while doing lengthy calculations of absolute value equations manually.
- It can solve various types of algebraic expressions that are present inside the mode.
- Our calculator with absolute value can operate through a computer, laptop, or mobile to find the absolute value equation.
- This absolute value functions calculator has a user-friendly interface so that you can solve it easily.
- It provides accurate and precise results as per your given input of the absolute value equation.
- Our solver does not give a sign-up option before using the calculator which makes your calculation experience amazing.
- The absolute value equations calculator is an educational tool that gives you solutions in the step-by-step method so that you can easily grasp the concept of the absolute value equation.










