Introduction to Inequality to Interval Notation Calculator
Inequality to interval notation calculator is an online tool that helps you to find the algebraic inequality equation. It also computes the linear equation and finds the value of x and the value of x on an interval represented on the number line.

Our inequality interval notation calculator also determines the your particular interval is open, closed, semi-open semi-closed, etc on a graph or number line.
What is Inequality Interval Notation?
Inequality interval notation is used to display the linear equation solution on a number line or graph. You can separately represent the variable value or you can combine two variable values and then display them on a number line.
Rule of Inequality Notation to Interval Notation:
Inequality Interval notation has different rules according to the inequality sign you tell whether the given interval is strictly bounded or unbounded on the graph or number line. The inequality to interval notation calculator follows some rules that are given,
Closed Intervals
a, and b are real numbers but both points' boundary values are not included
$$ [ x|a \lt x \lt b ] \; \; \; \; \; \; (a,b) $$
Open Interval
Although a, and b are real numbers both points' boundary values are included on the graph.
$$ [ x|a \le x \le b ] \; \; \; \; \; \; \; [a,b] $$
Semi-Open Interval
Here a is the not bounded and b is the bounded interval whereas a and b are real numbers
$$ [x|a \le x \le b ] \; \; \; \; \; \; [a.b] $$
Semi-Closed Interval
The semi-closed interval in the inequality to interval notation calculator is,
$$ [ x|a \lt x \le b ] \; \; \; \; \; \; \; (a,b) $$
Here b is not bounded and a is the in-bounded interval because a and b are real numbers
Compound Interval
Compound interval is the combination of two variables values that may or may not be bounded interval.
$$ [ x|x \lt a \;and\; x \gt b ] \; \; \; \; \; \; \; (- \infty, a) \cup (b, \infty) $$
Strictly Unbounded
All the real numbers in inequality interval notation calculator are bounded but their boundary points are not included on a graph or number line.
$$ [x|x \;is\;all\;real\; numbers] \; \; \; \; \; \; (-\infty, \infty) $$
One Side Closed Interval (On the Positive Side on a Number Line)
All the real numbers are greater than a but a is not included on a number line or graph
$$ [x|x \gt a ] \; \; \; \; \; \; \; \; (a, \infty) $$
One Side Closed Interval (On the Negative Side on a Number Line)
All the real numbers are less than b and b is not included on a number line or graph
$$ [x|x \lt b ] \; \; \; \; \; \; \; (-\infty, b) $$
One Side Semi-Open Interval (On the Positive Side on a Number Line)
All the real numbers are greater than or equal to a and a is included on a number line or graph
$$ [x|x \ge a] \; \; \; \; \; \; \; \; \; [a, \infty] $$
One Side Closed Interval
All the real numbers are less than or equal to b and b is included but a is not included on a number line or graph
$$ [x|x \le b] \; \; \; \; \; \; \; \; \; (-\infty, b) $$
Evaluation Process of Inequality Interval Notation Calculator
Convert to interval notation calculator can solve one side linear equation for a specific variable or compound inequality where two linear equations are solved with one single similar variable. It is because our calculator has updated features on its server.
When you give the input value in the calculator, it will check whether the given linear equation has compound inequality or not. After checking the given equation behaviour it calculates the inequality equation as we find the usual linear equation variable value.
If the given input is in a compound inequality equation then find the first linear equation and then find the second linear equation. After finding the solution of both the given linear equations merge both the solutions.
Lastly, Inequality to interval notation calculator represents the given solution on the number line or graph as per the interval behavior that tells whether the given function is bounded or unbounded.
Let's see some examples of one-sided or compound inequality linear equations along with their solution or graphical representation for a better understanding of this concept.
Inequality Notation to Interval Notation - Example
Inequality to internal notation examples with the solution of complete step by step explanation is given below,
Example of a Compound Inequality
Solve the following,
$$ 5 - 3x \le -1 or 8 + 2x \le 5 $$
Solution:
$$ 5 - 3x \le -1 \; \; \; \; \; \; or\; \; \; \; 8 + 2x \le 5 $$
Find each inequality
$$ 5 - 3x \le -1 \; \; \; \; \; \; \; \; 8 + 2x \le 5 $$
$$ -3x \le -6 \; \; \; \; \; \; 2x \le -3 $$
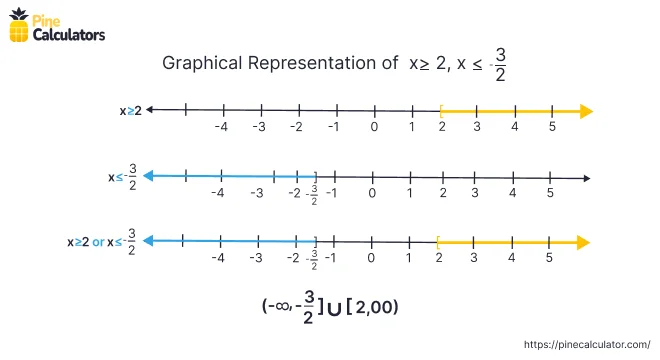
$$ x \ge 2 \; \; \; \; \; \; x \le -\frac{3}{2} $$
The graphical representation of the above example is given,
Example of One Sided Inequality
Find the following:
$$ -4 \le 3x - 7 \lt 8 $$
Solution:
$$ -4 \le 3x - 7 \lt 8 $$
Adding 7 to all parts:
$$ -4 + 7 \le 3x - 7 + 7 \lt 8 + 7 $$
$$ 3 \le 3x \lt 15 $$
Now divide each by 3,
$$ \frac{3}{3} \le \frac{3x}{3} \lt \frac{15}{3} $$
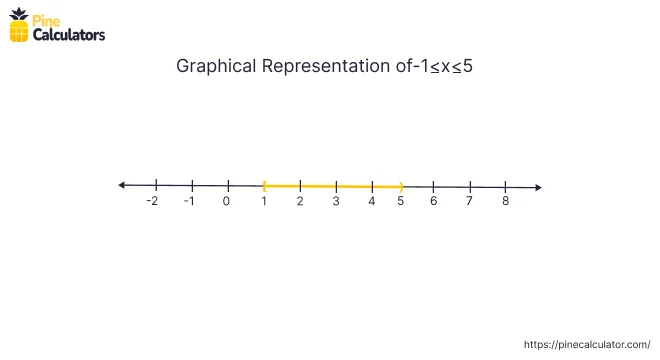
$$ 1 \le x \lt 5 $$
The graph of this solution is,
Example:
Solve the following,
$$ 6x - 3 \lt 9 \; and\; 2x + 7 \ge 3 $$
Solution:
$$ 6x - 3 \lt 9 \; \; \; \; \; and \; 2x + 9 \ge 3 $$
$$ 6x - 3 \lt 9 \; \; \; \; \; 2x + 9 \ge 3 $$
$$ 6x \lt 12 \; \; \; \; \; \; 2x \ge -6 $$
$$ x \lt 2 \; \; \; \; \; x \ge -3 $$
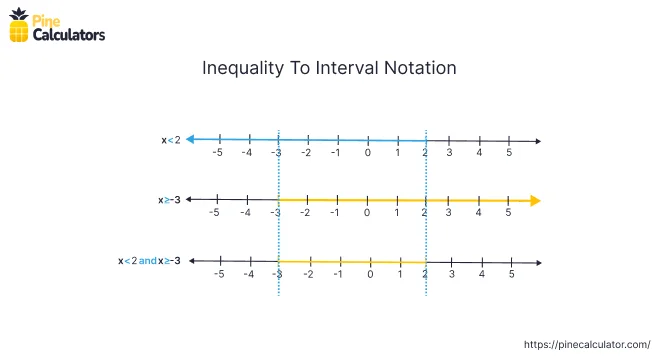
How to Use Inequality to Interval Notation Calculator
Inequality interval notation calculator has a user-friendly interface so that you can use it to calculate the linear function in less than a minute.
Before adding the input value to the convert to interval notation calculator, you must follow some instructions so that you do not experience any type of trouble in the evaluation process. These steps are:
- Choose the type of equation from One-sided or compound-sided
- Enter the linear equation along with the inequality value in the relevant field.
- Enter the second linear equation along with the inequality value in the relevant field. If you choose compounded interval then add a second equation otherwise no need to add to the calculator.
- Choose the variable which variable value you want to evaluate.
- Click the “Calculate” button to get the desired result of your given equation
- If you are trying our calculator for the first time then you can use the load example that gives you better clarity about its working procedure.
- Click on the “Recalculate” button to get a new page for solving more Inequality notation to interval notation problems.
Final Result from Convert to Interval Notation Calculator
Inequality to interval notation calculator gives you the solution in positive or negative real roots when you add the input to it. It provides you with solutions in a step-wise process in less than a minute. It may contain as
- Result option gives you a solution for a linear equation
- Possible step provides you with all the steps of the problem of the positive or negative root of a linear equation
- Plot provides you solution in the form of a graph or number line where intervals are defined.
Advantages of Using our Calculator
Convert to interval notation calculator will give you tons of benefits whenever you use it to calculate the linear inequality equation problem of an algebraic function. Its benefits are:
- lt saves time and effort from doing complex calculations of Inequality notation to interval notation problems
- The inequality interval notation calculator is a free-of-cost tool so you can use it for free to find the variable value in positive or negative real numbers
- It is a versatile tool that allows you to solve various types of Inequality interval notation of given linear inequality equation.
- It is a trustworthy tool that provides you with accurate solutions every time whenever you use it to find the Inequality notation to interval notation calculation.
- You can use this Inequality to interval notation calculator for practice so that you get a strong hold on Inequality interval notation for linear equations problems.









